igerx.blogg.se - Khan academy absolute value inequalities

concepts such as estimation, percent, ratio, rate, absolute value, the number line, decimal representation and sequences of numbers.

arithmetic operations, exponents and roots.

properties and types of integers, such as divisibility, factorization, prime numbers, remainders and odd and even integers.

The skills, concepts and abilities are assessed in the four content areas below. Many of the questions are "word problems," which must be translated and modeled mathematically.

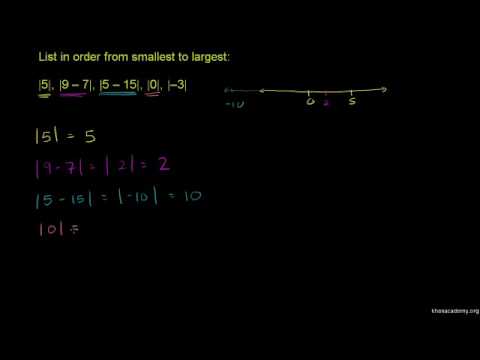
If you are getting the hang of this, move on the Got It? section to practice your skills.Some of the Quantitative Reasoning questions are posed in real-life settings, while others are posed in purely mathematical settings.

Take a moment to watch the KHAN Academy video Absolute value inequalities | Linear equations | Algebra | Khan for further instruction on this topic: If the problem is asking for less than or equal to, or greater than or equal to, then your circles will be closed (filled in). So remember, if the problem is only asking for less than or greater than, your circles will be open (not filled in). If it were asking for ≤ 12, you could have filled the circles in. The reason for this is that the original problem was asking for < 12. Notice that the circles you placed on each of those numbers are open there is not fill inside like the circle on 0.

Take a look at your number line where you drew the line between -12 and 12. It is the range of numbers on the number line where the answer can be found. |x| -12 and x < 12.įinally, the formal way to write the answer to this problem is -12 < x < 12. Put the problem into words you can understand. An inequality will have a greater than sign (>), a less than sign ( This will be the example problem for this part of the lesson on how to solve an absolute value inequality: |x| (This is a one-step inequality problem).įirst, you need to be aware that the example problem is referred to as an inequality, NOT an equation! An equation will have an equals sign in it (=). (If you need a refresh on these topics, review our lessons found under Additional Resources in the right-hand sidebar first.) Inequality simply means things are not equal. The absolute value of a number is its distance from 0 regardless of which direction (positive or negative). Today you are going to learn how to solve absolute value inequalities so you can solve problems just as challenging as that one! The opening problem to this lesson seems a little daunting, doesn't it?